GECCO 2003 - LNCS 2723

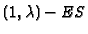
Dimension-Independent Convergence Rate for Non-isotropic $(1,\lambda)-ES$

Anne Auger^1,2, Claude Le Bris^1,3, and Marc Schoenauer²

¹CERMICS - ENPC
Cité Descartes, 77455
Marne-La-Vallée, France
{auger,lebris}@cermics.enpc.fr

²INRIA Rocquencourt,
Projet Fractales
BP 105, 78153 LE CHESNAY Cedex, France
marc.schoenauer@inria.fr

³INRIA Rocquencourt,
Projet MIC MAC
BP 105, 78153 LE CHESNAY Cedex, France

Abstract. Based on the theory of non-negative super martingales, convergence results are proven for adaptive $(1,\lambda)-ES$ (i.e. with Gaussian mutations), and geometrical convergence rates are derived. In the d-dimensional case (), the algorithm studied here uses a different step-size update in each direction. However, the critical value for the step-size, and the resulting convergence rate do not depend on the dimension. Those results are discussed with respect to previous works. Rigorous numerical investigations on some 1-dimensional functions validate the theoretical results. Trends for future research are indicated.

LNCS 2723, p. 512 ff.

Full article in PDF