An Analysis of the (+1) EA on Simple Pseudo-Boolean Functions

Carsten Witt^*

Abstract. Evolutionary Algorithms (EAs) are successfully applied for optimization in discrete search spaces, but theory is still weak in particular for population-based EAs. Here, a first rigorous analysis of the (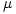 + 1) EA on pseudo-Boolean functions is presented. For three example functions well-known from the analysis of the (1 + 1) EA, bounds on the expected runtime and success probability are derived. For two of these functions, upper and lower bounds on the expected runtime are tight, and the ( 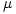+ 1) EA is never more efficient than the (1 + 1) EA. Moreover, all lower bounds grow with 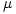. On a more complicated function, however, a small increase of  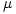provably decreases the expected runtime drastically.

For the lower bounds, a novel proof technique is developed. The stochastic process creating family trees of individuals is investigated and relationships with well-known models of random trees, e. g., uniform random recursive trees, are established. Thereby, a known theory on random trees is transferred to the analysis of EAs. Moreover, generalizations of the technique are applicable to more complex population-based EAs.

^*supported by the Deutsche Forschungsgemeinschaft (DFG) as a part of the Collaborative Research Center “Computational Intelligence” (SFB 531)

LNCS 3102, p. 761 ff.

Full article in PDF

lncs@springer.de
© Springer-Verlag Berlin Heidelberg 2004