Simultaneity Matrix for Solving Hierarchically Decomposable Functions

Chatchawit Aporntewan and Prabhas Chongstitvatana

Abstract. The simultaneity matrix is an 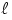× 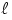matrix of numbers. It is constructed according to a set of 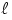-bit solutions. The matrix element m_ij is the degree of linkage between bit positions i and j. To exploit the matrix, we partition {0, ..., 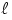–1} by putting i and j in the same partition subset if m_ij is significantly high. The partition represents the bit positions of building blocks (BBs). The partition is used in solution recombination so that the bits governed by the same partition subset are passed together. It can be shown that by exploiting the simultaneity matrix the hierarchically decomposable functions can be solved in a polynomial relationship between the number of function evaluations required to reach the optimum and the problem size. A comparison to the hierarchical Bayesian optimization algorithm (hBOA) is made. The hBOA uses less number of function evaluations than that of our algorithm. However, computing the matrix is 10 times faster and uses 10 times less memory than constructing Bayesian network.

LNCS 3102, p. 877 ff.

Full article in PDF

lncs@springer.de
© Springer-Verlag Berlin Heidelberg 2004