 |
    |
Upper Bounds on the Time and Space Complexity of Optimizing Additively Separable Functions
Matthew J. Streeter
Computer Science Department and Center for the Neural Basis of Cognition, Carnegie Mellon University, Pittsburgh, PA 15213matts@cs.cmu.edu
Abstract. We present upper bounds on the time and space complexity of finding the global optimum of additively separable functions, a class of functions that has been studied extensively in the evolutionary computation literature. The algorithm presented uses efficient linkage discovery in conjunction with local search. Using our algorithm, the global optimum of an order-k additively separable function defined on strings of length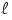 
can be found using O( 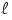ln(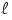)2k) function evaluations, a bound which is lower than all those that have previously been reported.
LNCS 3103, p. 186 ff.
lncs@springer.de
© Springer-Verlag Berlin Heidelberg 2004